Ragmania
Supersnelle anagrammenzoeker

De Nederlandse taal is rijk aan anagrammen. Volgens Hugo Brandt Corstius (absurd ontuchtig ros, 1935-2014) telt het Nederlands meer dan drie­honderd­duizend anagram­woorden, woorden dus die één ander woord opleveren. Anagrammen van meer dan één woord zijn er nog veel meer.

Er zijn in Nederland dan ook verschillende mensen die de computer hebben ingeschakeld om zoveel mogelijk anagrammen te zoeken. Battus, oftewel Hugo Brandt Corstius (schudt naburig torso) is de pionier (zie paragraaf ua in zijn meesterlijke Opperlans!). Onno Zweers (Noors wezen) schreef in 1996 het Windows-programma Maanrag, en Raymond Zand­bergen (zo'n brandygendarme) maakte een in veel opzichten verbeterde variant voor Linux, Ragmaan 2. Bovendien heeft de Van Dale op cd-rom ook een ingebouwde anagrammen­zoeker.

Is er dan ruimte voor nog een andere zang naar ommekeer (ana­gram­men­zoeker)? Misschien niet, maar het is nu te laat: ik heb er ook al een gemaakt.

De onmiddellijke aanleiding was dat ik plotseling merkte dat Maanrag niet werkt op nieuwere Windows-systemen. Het programma verslikt zich in de grote geheugen­om­vang die tegenwoordig gebruikelijk is. Van maker Onno Zweers kreeg ik in juli 2003 een e-mailtje waaruit bleek dat we niet op een nieuwe versie hoeven rekenen, omdat de bron­bestan­den verloren zijn gegaan.

Het alternatief van Raymond Zand­bergen is voortreffelijk, maar alleen weggelegd voor Linux-gebruikers. Die gunnen we natuurlijk van harte hun voordeel, maar Windows-gebruikers willen ook weleens een anagram zoeken (zakenman: armoe eng!).

Ik stond paf (stond pik af)

De tweede aanleiding komt weer van Hugo Brandt Corstius (drastisch, onguur, bot). In Opperlans! schrijft hij over zijn eerste project om de Neder­landse taal na te vlooien op ana­grammen.

'Daar had ik iets moois voor verzonnen. Ik gaf aan elke letter een getalwaarde, altijd een priemgetal. (...) Bij elk woord vermenigvuldig je de getalwaarden van de letters met elkaar. (...) Woorden met dezelfde getalwaarde zijn anagrammen van elkaar, want producten van dezelfde priemgetallen.'

Ik mag wel zeggen dat ik door deze passage diep getroffen was. Ik stond paf. Wat een geniaal idee! En wat een prachtig samengaan van wiskunde en taalkunde!

Met de priem­getallen­truc zou een anagrammen­zoeker (zomergraan kan mee!), vele malen sneller zijn dan eentje die de teksten van woorden vergelijkt, zelfs al worden daartoe eerst de letters alfabetisch gerangschikt. Ik wilde weleens weten hoe veel sneller.

Vandaar dus Ragmania, mijn nogal Spartaans uitgevoerde, maar razendsnelle ana­gram­men­zoe­ker op basis van een idee van HBC. De zoekmachine van Ragmania is bijna tien keer zo snel als eentje die woorden vergelijkt op basis van de gesorteerde letters.

Battuslading (bilnaad gutst)

De vermenigvuldigde letter-priemgetallen noem ik de battuslading van een woord. Ragmania heeft een grote woordenlijst en weet van ieder woord de battuslading. Van het op anagrammen te onderzoeken woord berekent Ragmania ook de battuslading. Dan zoekt het programma totdat het een battuslading heeft gevonden waardoor die gedeeld kan worden, zonder dat er een rest overblijft. Het quotiënt is de battuslading van de overgebleven letters. Als het 1 is, hebben alle letters een evenknie gevonden en is een anagram gevonden. Is het ongelijk aan 1, dan zijn er nog letters die geen onderdak hebben, en zoekt Ragmania verder met het quotiënt.

Tijdens het zoekproces wordt dus helemaal niet naar de eigenlijke letters gekeken, maar alleen naar de deelbaarheid van de battus­ladings­getallen (belastinggeld staat nul, lang­benigste lust daalt, dan betaalt slungeligst!). Omdat het delen van twee getallen voor de computer één stap is, en het vergelijken van reeksen letters gedaan wordt in een groter aantal stappen, gaat het zo snel.

Haken en ogen (hé, geen kanon)

Er zitten overigens aan de priem­getallen­truc (meercellig nat prut) wel haken en ogen. Het belangrijkste is dat de getallen te groot worden om zelfs door de hedendaagse, krachtige computers verwerkt te worden. Eigenlijk denk ik dat Battus zijn vernuftige inval dan ook voornamelijk als grap bedoeld heeft. Computers kunnen wel rekenen met grotere getallen, maar dan wordt het allemaal een stuk trager en is het nog maar de vraag of er een voordeel ten opzichte van directe tekst­ver­ge­lij­king blijft bestaan.

Vandaar dat de battuslading van een woord in Ragmania niet bestaat uit één product van priem­getallen, maar uit vier producten. Om te controleren of een woord is bevat in een ander, moeten we kijken of de vier priem­getallen uit de battus­lading daarvan deel­baar zijn door die van het woord. Als één deling niet uitkomt, weten we dat het niet past en hoeven we de eventuele over­gebleven delingen niet meer uit te voeren. Ana­grammen­zoeker = omzagen rekenraam!

Om de getallen laag te houden, gebruiken we de kleinste priem­getallen: 2, 3, 5, 7, 11, 13 en 17. In het eerste priem­product van de battus­lading zit alleen de informatie over de letters t, i, h, u, b, y en q. In het tweede alleen de informatie over a, o, g, k, c, j en x, in het derde over n, d, l, m, p en f, en in het vierde over e, r, s, v, w en z. De letters zijn zo verdeeld dat ieder priem­product ongeveer evenveel vaak voor­komende als zeld­zame letters onder zijn hoede heeft. Door het zo in te richten, kan Ragmania uit de voeten met combinaties van woorden tot zo'n dertig, veertig letters.

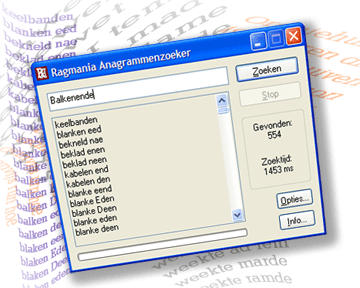
Ragmania gebruiken (maak rare buigingen)

Ragmania is een stokoud programmaatje. Het stamt al uit 2003, kun je nagaan! Maar, eigenlijk tot mijn verbazing: het werkt nog steeds.

Het gebruiken van Ragmania wijst zich zelf, lijkt me. Het werkt onder Windows 98 tot en met 7, en waar­schijn­lijk ook wel onder Windows 8. De download (939 kB) bevat een installatie­program­maatje (in het Engels, sorry). De download bevat ook de bronbestanden, zodat de ingewijde kan nagaan hoe ik het in elkaar gepeuterd heb. Wie erop is uitgekeken, kan het op de gebruikelijke manier via het configuratie­scherm van Windows verwijderen.

Wees voorbereid op duizeling­wekkende aantallen vondsten, waarvan de meeste niet erg interessant zijn. Maar sommige andere wel degelijk!

Download Ragmania (.msi-file, 939 kB)

Frequent Aangekaarte Questies